Mahya Hajihassanpour

Mahya Hajihassanpour

I am an engineer, mathematician, and scientist working as a computational science specialist.

Structured and unstructured grid generation techniques (Fortran)

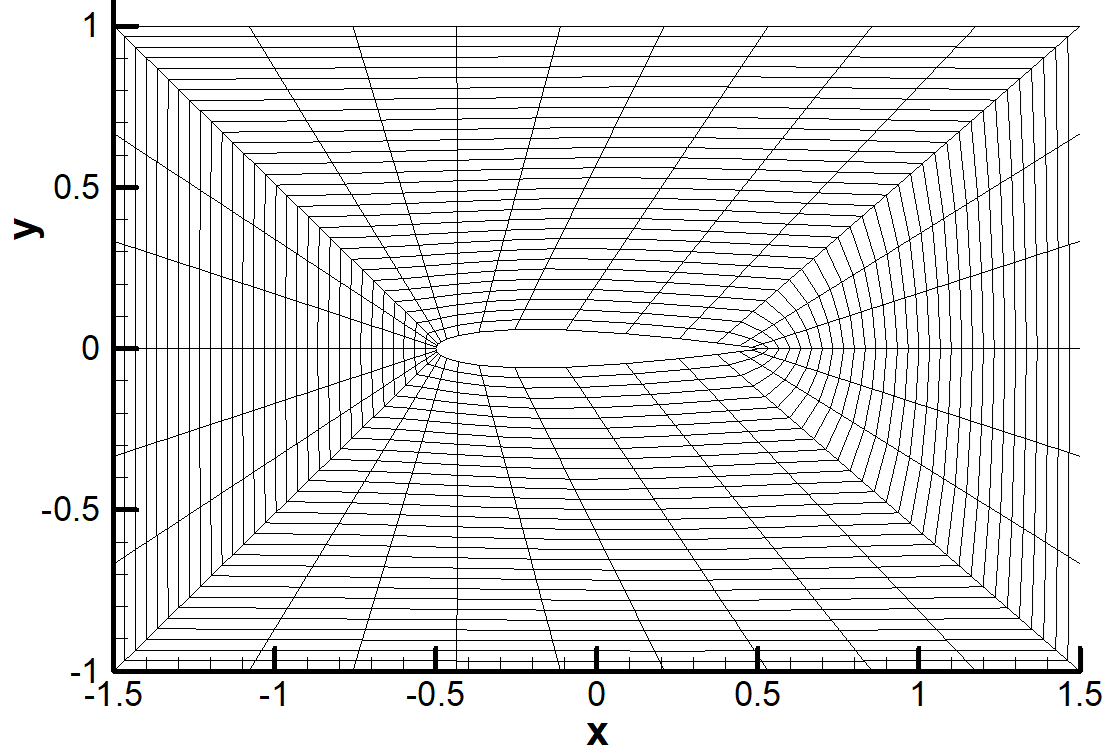
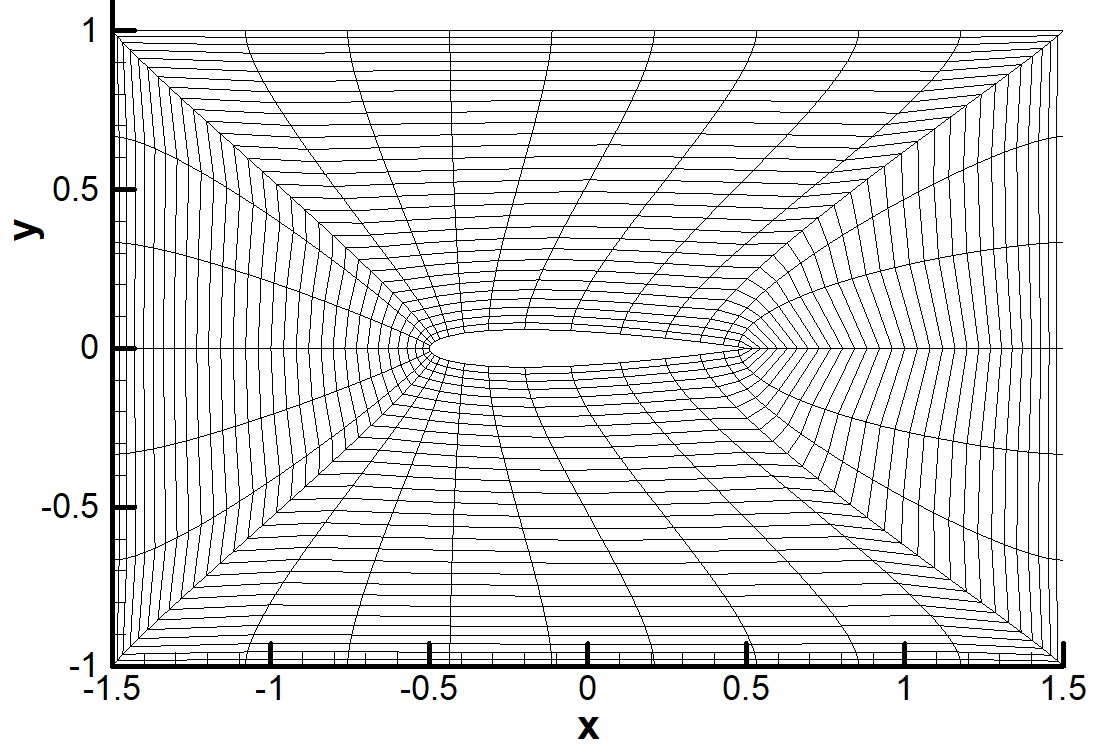
structured grid

Different algebraic grid generation methods are written in Fortran as follow:

  • Lagrange lagrange
  • Hermit lagrange
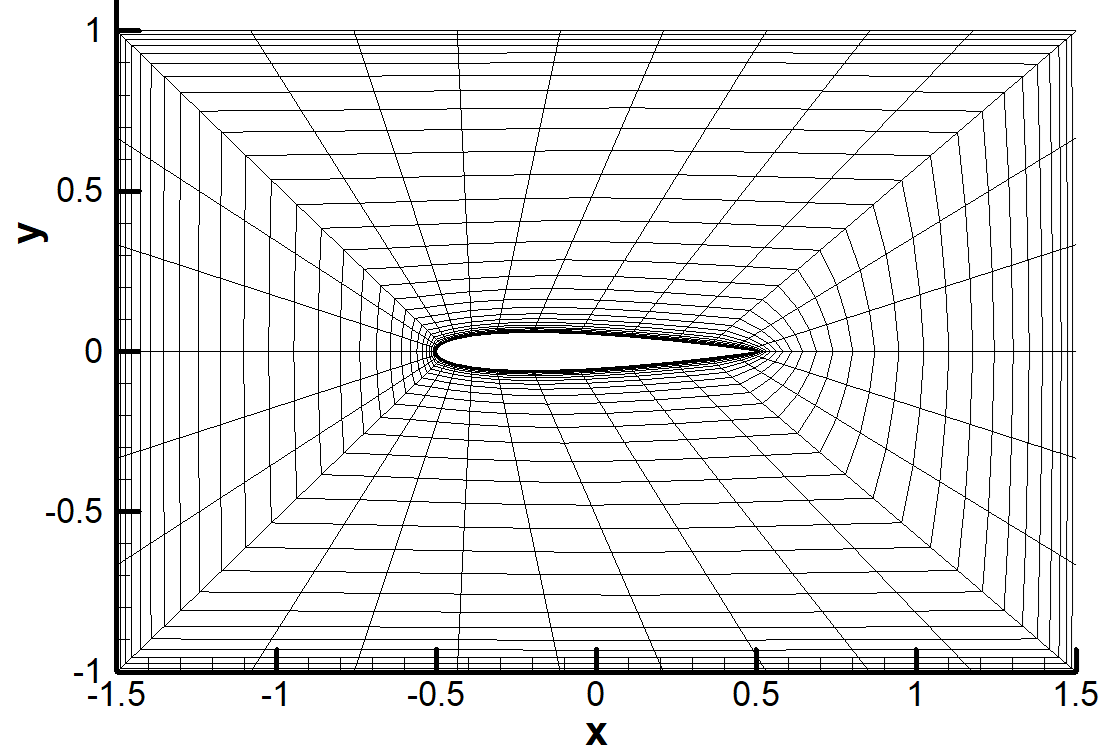
  • Tow-Sided Hyperbolic Tangent (Vinkour Streaching Function) lagrange
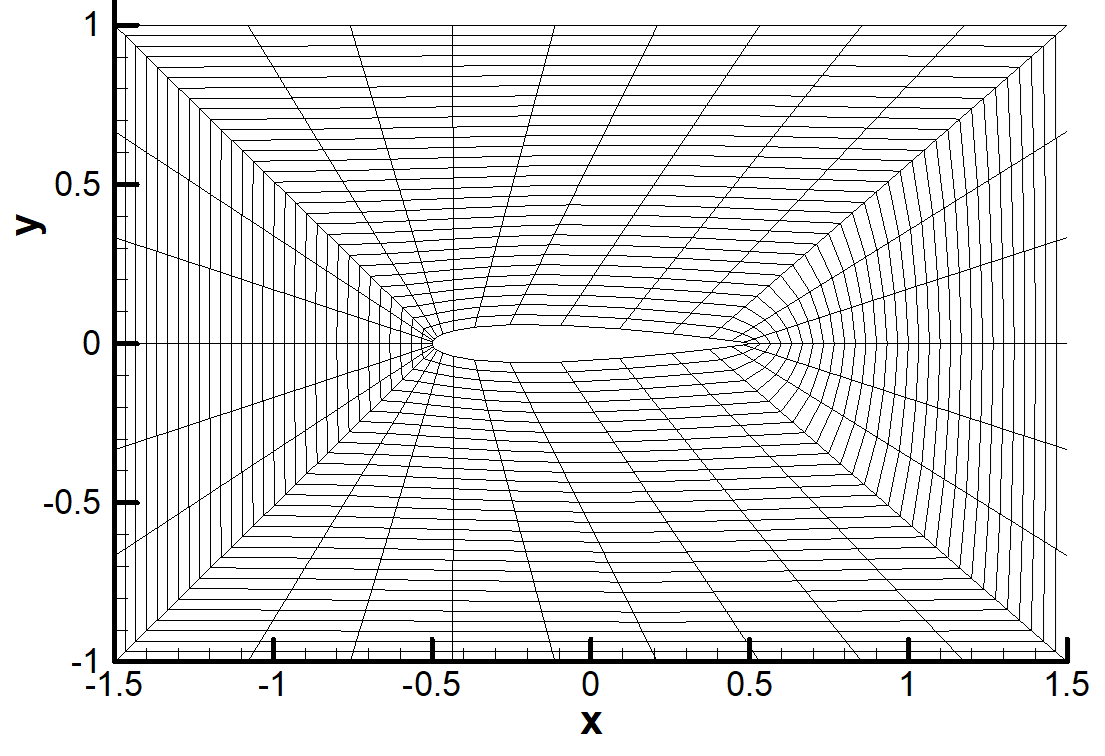
  • Transfinite (TFI) lagrange

Moreover, Poisson equation is solved using finite difference methods to generate smooth grids with orthogonality on the surface of arbitrary 4-digit airfoils. This method is called the elliptic grid generation and its code is written in Fortran.

  • Elliptic grid generation

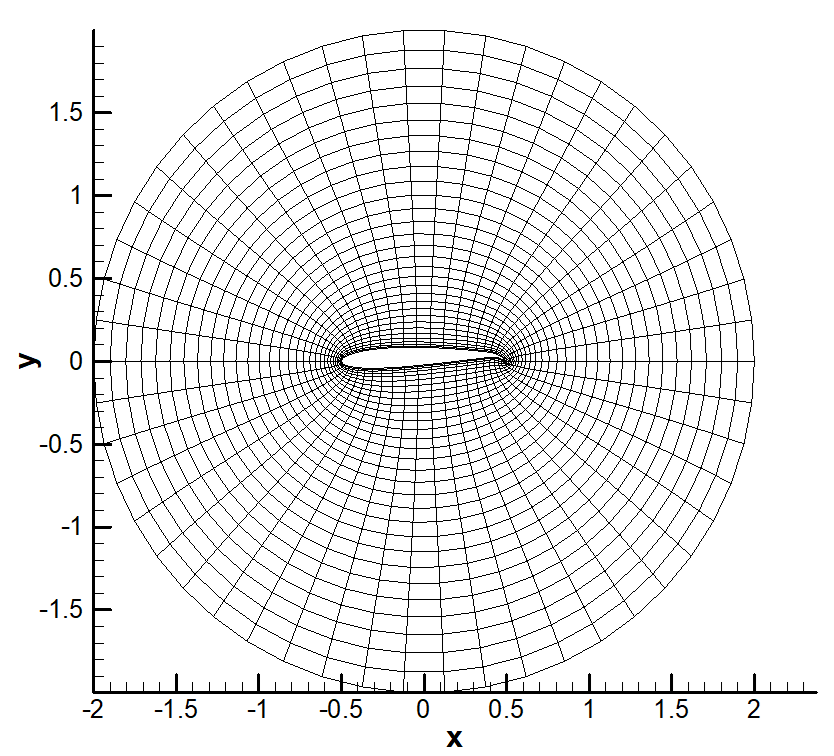
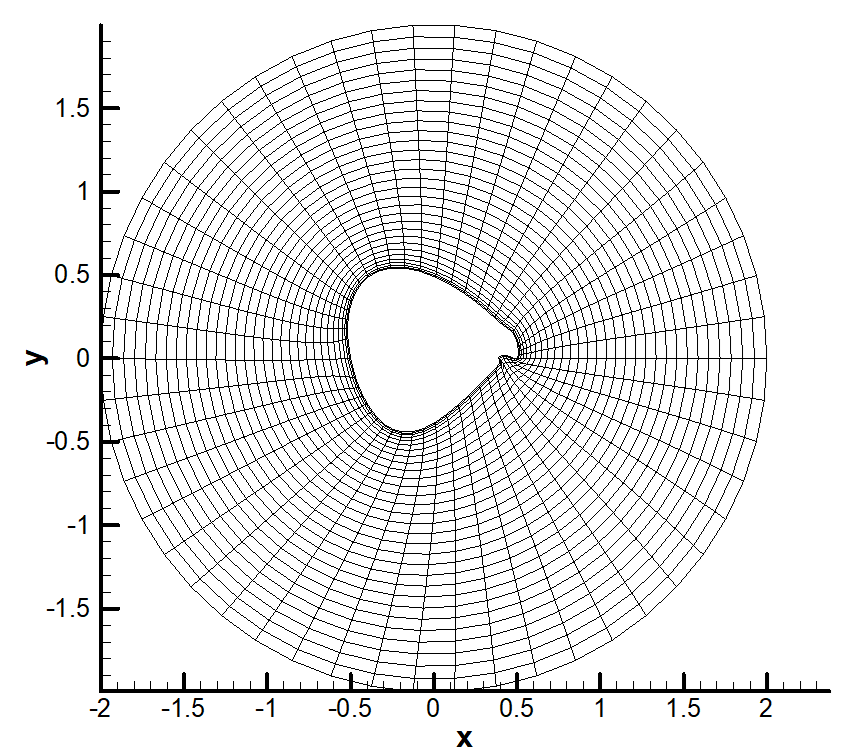
elliptic_thin elliptic_thick

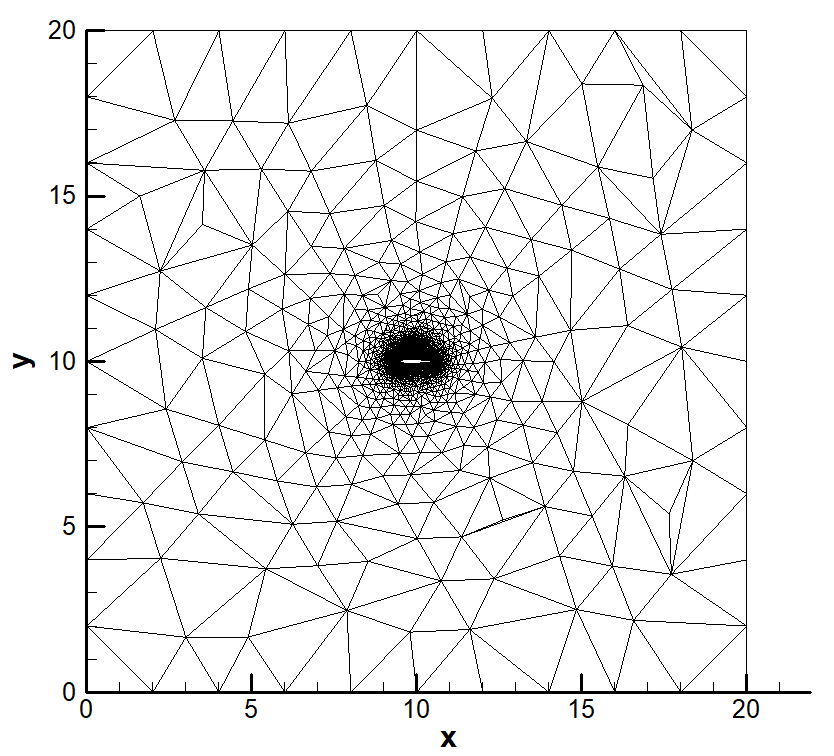
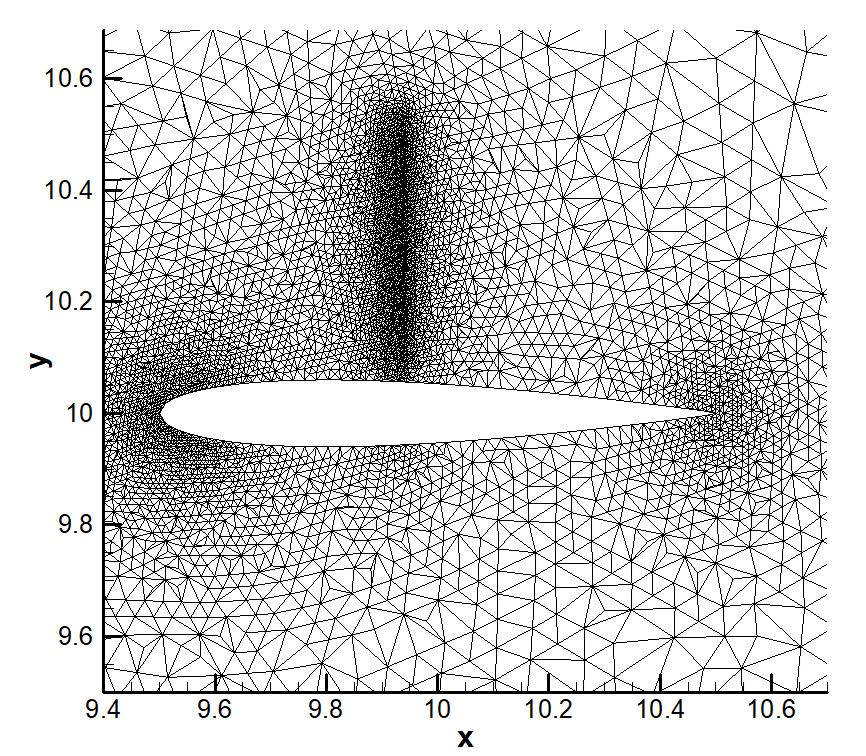
Unstructed grid generation

  • Advancing front using point and line sources

Advancing front grid generation can be used to generate unstructured triangular meshes with the ability to control the mesh length locally. The control can be done using background mesh with point and line sources with their associate strength to refine mesh around them locally. The role of the background mesh is to locally control the length of triangles. The background mesh is obtained by solving Poisson equation using finite difference method. The code is written in Fortran. advancing_front_zoon_out advancing_front_zoon_in